Canvas系列（7）：形变

发表于 | 分类于 |

CSS3中有一个很重要的点，就是形变。他分为移动，缩放、旋转和倾斜。在Canvas中，形变都是基于坐标做的，所以，并没有直接的API支持倾斜，其它几种都是有独立的API来支持，命名和CSS是一样的。今天我们就看一下这几种吧。

平移

平移是最简单的一种形变，我们直接来看一个例子吧：

1
2
3
4
5
6
7
8
context.fillRect(10,10,20,20);

// x平移20px y平移20px
context.translate(20, 20);
context.fillRect(10,10,20,20);

context.translate(20, 20);
context.fillRect(10,10,20,20);

效果：

平移形变

通过上面我们可以看到，平移（形变）移动的是坐标系，移动以后会以新的坐标系进行绘图，当多次平移（形变）以后每次都会以上一次的坐标系为准。此时你可能会问，那形变不是很危险吗，每次使用了形变就会使用新的坐标系，以后所有绘制的图片都会受到影响？没错是这样的，那改怎么解决呢？还记得之前的状态吗？现在给一个简单的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
// 形变前往往需要保存状态
context.save();

context.translate(20, 20);
context.fillRect(10,10,20,20);

// 形变结束，恢复之前的状态
context.restore();

// 此时以之前的坐标系绘制
context.beginPath();
context.fillStyle='red';
context.fillRect(10,10,20,20);

效果：

使用保存状态

缩放

缩放也是相对于坐标系来说的，看一下这个例子：

1
2
3
4
5
6
7
8
9
10
11
context.strokeStyle='red';
context.lineWidth=10;
context.strokeRect(20, 20, 50, 50);

context.beginPath();
// x是原来的1.5倍 y是原来的1.5倍
context.save();
context.scale(1.5, 1.5);
context.strokeStyle='blue';
context.strokeRect(20, 20, 50, 50);
context.restore();

效果：

缩放

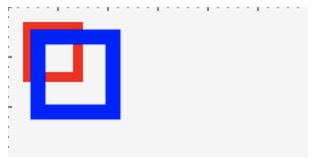
可以看到，缩放改变的也是坐标系，在新的坐标系系中，宽度也放大了，一个像素已经不再是真正的一个像素了，而是放大以后的大小。所以可以看到都是10个像素的边框，宽度也不一样了。需要注意的是缩放的值大于1的时候是放大，0~1之间是缩小，1和原来是一样大的。

旋转

直接上代码：

1
2
3
4
5
6
7
8
9
10
11
12
context.strokeStyle='red';
context.lineWidth=10;
context.strokeRect(80, 20, 50, 50);

context.beginPath();
// x是原来的1.5倍 y是原来的1.5倍
context.save();
context.rotate(Math.PI / 180 * 45);

context.strokeStyle='blue';
context.strokeRect(80, 20, 50, 50);
context.restore();

效果：

旋转

可以看到旋转是基于坐标的原点的，如果不希望按照原点旋转的话，可以先平移再旋转。另外旋转也是根据弧度来旋转的而不是角度。

矩阵变换

矩阵变换使用的API是context.transform(a, b, c, d, e, f);，所对应的矩阵的位置是下面这个样子：

$$\left[
\begin{matrix}
a & c & e \\
b & d & f \\
0 & 0 & 1
\end{matrix}
\right] $$

什么，看不懂？前方高能！！！多年前欠下的线性代数债，现在要还了。

对于形变，假设开始的坐标是(\(x_0\),\(y_0\)，结束的坐标是(\(x_1\),\(y_1\))，那么假如(\(x_1\),\(y_1\))是\(x_0\)平移了e个单位，\(y_0\)平移了f个单位后得到的结果，那么\(x_1\)和\(y_1\)就等于如下：
$$
x_1 = x_0 + e \\
y_1 = y_0 + f
$$

使用矩阵的笛卡尔积（左边值的第几行第几列中的值，就是右边第一个矩阵的第几行与第二个矩阵的第几列的乘积之和就是）的样子就是这个样子：

$$\left[
\begin{matrix}
x_1 \\
y_1 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
1 & 0 & e \\
0 & 1 & f \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$

上面矩阵是平移时候的矩阵，将中间的矩阵带入矩阵的API有：context.transform(1, 0, 0, 1, e, f);。也就是说context.translate(e, f);等价于context.transform(1, 0, 0, 1, e, f);。

对于缩放，同样假设开始的坐标是(\(x_0\),\(y_0\))，结束的坐标是(\(x_1\),\(y_1\))，那么假如\(x_0\)缩放了a个单位，\(y_0\)缩放d个单位，那么\(x_1\)和\(y_1\)就等于如下：
$$
x_1 = a * x_0 \\
y_1 = d * y_0
$$

使用矩阵的笛卡尔积就是这个样子：

$$\left[
\begin{matrix}
x_1 \\
y_1 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
a & 0 & 0 \\
0 & d & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$

也就是说context.scale(a, d);等价于context.transform(a, 0, 0, d, 0, 0);。

旋转有点复杂，坐标(\(x_0\),\(y_0\))和(\(x_1\),\(y_1\))的意义和上面一下，旋转有如下公式（可以自行推到，并不难）：

$$
x_1 = x_0 * cos\theta - y_0 * sin\theta \\
y_1 = x_0 * sin\theta + y_0 * cos\theta
$$

使用矩阵的笛卡尔积就是这个样子：

$$\left[
\begin{matrix}
x_1 \\
y_1 \\
1 \\
\end{matrix}
\right] =
\left[
\begin{matrix}
cos\theta & -sin\theta & 0 \\
sin\theta & cos\theta & 0 \\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_0 \\
y_0 \\
1 \\
\end{matrix}
\right] $$

也就是说context.rotate(angle);等价于context.transform(cos(angle), sin(angle), -sin(angle), cos(angle), 0, 0);。

所以我们上面的几个例子，我们做下面的等价替换，效果是一样的：

1
2
3
4
5
6
7
8
9
10
11
12
context.translate(20, 20);
// 等价于
context.transform(1, 0, 0, 1, 20, 20);

context.scale(1.5, 1.5);
// 等价于
context.transform(1.5, 0, 0, 1.5, 0, 0);

context.rotate(Math.PI / 180 * 45);
// 等价于
var theta = Math.PI / 180 * 45;
context.transform(Math.cos(theta), Math.sin(theta), - Math.sin(theta), Math.cos(theta), 0, 0);

除了transform外还有一个矩阵变换的方法叫setTransform，参数是一模一样的context.setTransform(a, b, c, d, e, f);。两者的区别是后者始终以最初的坐标做为参照，而transform以上次变换后的坐标做为参照（类似于前面的三个API）。

-------------本文结束 感谢您的阅读-------------
0%